Today we went over more permutations and combinations examples which was excellent. Pictured below are examples that explain clearly the difference between
perms and
coms.
Of course, the most important thing to remember is that order matters in permutations so there are no 'doubles', while in combinations order doesn't matter. Thus, we "divide out the doubles", to speak Mr. Max's talk.

These slides show some "tricks" that are very useful for the questions in the exercises. The first is when there are identical objects. The idea is that you find all the options, then divide out wherever there are repeats, like in the word AARDVARK, where there is a repeat of 3 and a repeat of 2.
 http://www.cbc.ca/parents/showPics/arthur.jpg
http://www.cbc.ca/parents/showPics/arthur.jpg

This trick is in regard to circular permutations. The reasoning is that a circle has no beginning or end, which changes the rule. Also note the special rule for 3-D circles.

The third trick is in reference to when objects, usually people, must be or cannot be beside each other. For example, how can we seat the 4 Grade 12 precalculus girls if Anna must be beside Bethany and must not be beside Amy? Or, how many ways can we seat those same girls so that they won't disrupt the whole class?

Anyways, the big news in class today is that the test is going to be moved to
Thursday, April 24. This will give us another day to work on the exercises as well as the pretest.
Sometime this week we should also be recieving hard copies of some old exams. These will be great study material and should answer a lot of the questions we have about the exam.
Just a note, I was watching the hockey game (which Montreal won, by the way),and I heard Ron McLean use the word permutation. And I understood what he meant! So that was a bit of a eureka moment and an application of math in real life.
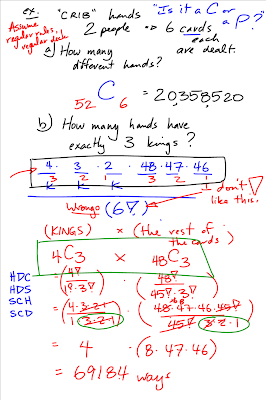
 The first example we saw was a continuation from yesterday. Here are two more solutions, one using a combination and one using a permutation.
The first example we saw was a continuation from yesterday. Here are two more solutions, one using a combination and one using a permutation.
 Here's another example showing how to use permutations to find probability. The reason it is a permutation is because the order matters in this case.
Here's another example showing how to use permutations to find probability. The reason it is a permutation is because the order matters in this case. This example is a similar question, but order doesn't matter, so we used a combination.
This example is a similar question, but order doesn't matter, so we used a combination. We also received the key for the pretest, so don't forget to prepare for the test tomorrow. Remember that we will be using calculators.
We also received the key for the pretest, so don't forget to prepare for the test tomorrow. Remember that we will be using calculators.